23.05.07 (set: 23.05.2007) ~ <<<
30.05.07 (set: 30.05.2007) ~ >>>
~ Dr. Dieter Porth - Göttingen
Kuddelowskis Lösung für den versteckten Pfad.
------------------------------
Pressemitteilung Kontaktlink zu Redaktion buergerstimmen.de [ Homepage ] (Dr. Dieter Porth)[Göttingen - 23.05.07] [Bericht]
Kuddelowskis geheimer Pfad - die Lösung
Die Lösung ist simpel.
0. Wer keinen Stadtplan hat, kann das Internet-Angebot der Stadt Göttingen nutzen (http://stadtplan.goettingen.de/), um sich einen Plan zu erstellen. Mit dem Schlagwort Kiesseestraße erhält man den richtigen Kartenausschnitt. Man muss dann lediglich den größten Maßstab wählen, um die Position bestimmen zu können
1. Man bestimmt auf dem Bild und auf der Karte die Entfernung zwischen zwei markanten Hochhäusern (Hochhaus am Ende vom Mittelberg und Wohnstift in der Charlottenburger Straße rechts und links des Baumes. Die beiden Häuser sind laut Karte ungefähr 380 m voneinander entfernt. Auf dem Bild sind es 748 Punkte Damit entsprechen zwei Punkte ungefähr einem Meter.
2. Man testet die Abschätzung an Hand der Geschosshöhen. Auf dem Foto ist ein Stockwerk ungefähr 5 Punkte hoch. Damit wäre ein Geschoss ungefähr 2,5 m hoch. Die ist etwas niedrig, und die Geschosshöhe wird auf etwa 2,8m geschätzt. Mit der Geschosshöhe kann man die Höhe des zehnstöckigen Gebäudes abschätzen mit (10 * 2,8m = ) 28m abschätzen.
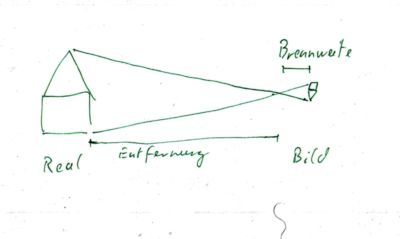
3. Nun nutzt man die Strahlensätze, um folgende Formel aufzustellen. Da man die Höhe des Hauses beim digitalen Foto nur in Punkten bestimmen kann, muss man die Punkte in Meter umrechnen. Hier hilft es, dass die Brennweite zwecks Vergleichbarkeit so angegeben wurde, wie man es bei einer Kleinbildkamera gewohnt ist. (In Realität ist die Brennweite der Optik viel geringer, weil der Fotochip viel kleiner als das Negativ einer Kleinbildkamera ist..):
Höhe des Gebäudes in Metern Punkte auf dem Chip Gesuchte Entfernung in Meter ------------------------------------- * ------------------------------ = ---------------------------------------------- Höhe des Gebäudes in Punkten Höhe des Chips in Meter Brennweite bei ausgefahrenen Zoom in Meter
Nun wurde das Foto bei maximalem Zoom aufgenommen. Die Brennweite betrug 106 mm, wenn das Negativ 24 mm hoch wäre. Dabei hat das Negativ in vertikaler Richtung aus 1704 Punkte. Die Höhe des zehn Stockwerke hohen Hauses schätzt man mit 28 Meter ab, wobei die zehn Stockwerke auf dem Bild aus 57 Punkten bestehen. Man setzt ein
10*2,8m 1704pt x ----------- * ------ = -------- 57 pt 0,024 , 0,106 m
und berechnet
x = 3700 m (zirka)
4. Da beide Hochhäuser auf dem Foto ungefähr gleich groß sind, sind sie auch beide ungefähr 3700 m vom Fotopunkt entfernt sind. Mit einem Zirkel bestimmt man auf der Karte den Fotopunkt. An Hand der Wegbeschreibung kann man dann die Position des Pfades abschätzen und so den Anfang des Pfades leicht finden.
------------------------------
Anmerkung
Kommentar: Am Ende war ich doch erstaunt, wie genau die Schätzung war. Dr. Dieter Porth.